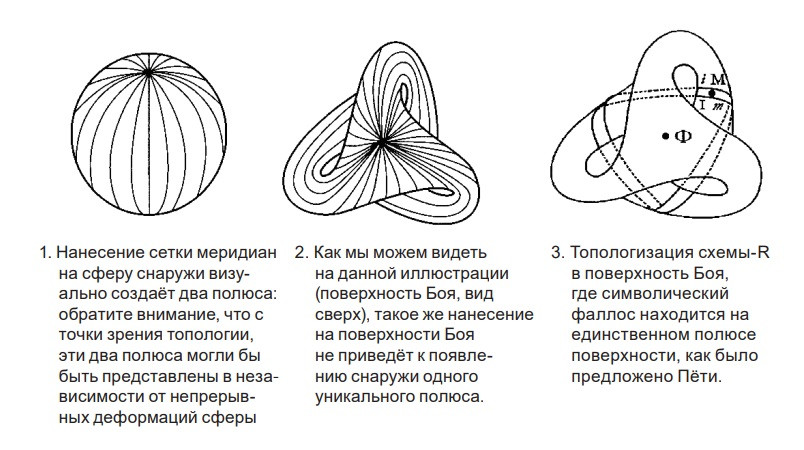
Фабрис Гийо, клинический психолог, доктор психоанализа на базе главного психиатрического центра госпиталя Жоржа Мазюреля (85), преподаватель факультета психологии Нанта; fabrice.guyod@univ-nantes.fr

Общение Жака Лакана с Жаном-Пьером Пёти в 1979 г. подтверждает только подписанное рукой Лакана пригласительное письмо. Насколько известно, не было обнаружено иных свидетельств истории этих трёх встреч[1] ни в речи Лакана, ни в созданных им впоследствии текстах.

[Прим.перев.: Жан-Пьер Пёти́ — французский учёный, специализирующийся в области механики жидкости, физики плазмы, магнитной гидродинамики, космологии и теоретической физики, cоздатель жанра научных комиксов.]

В любом случае наводки в отношении топологии, которые Пёти мог бы передать при встречах Лакану, оказались бы, в том числе и в наши дни, ценными. Они привели бы нас к серьезному вопросу: почему Лакан предпочёл топологизировать свою схему-R в поверхность кросс-кэпа, хотя Пёти предложил ему для этого поверхность Боя? Ведь Пёти исходил из того, что при погружении кросс-кэпа на его поверхности появляются две точки пинча, одну из которых Лакан ранее игнорировал.

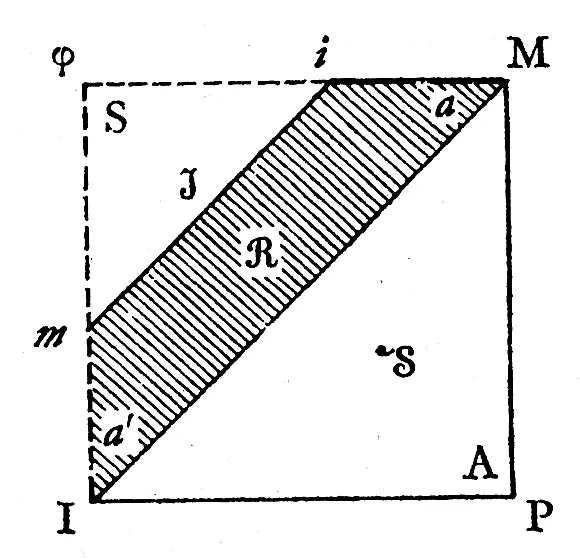
Обратимся к теоретическим и клиническим аспектам. При внимательном рассмотрении схема-R прочерчивает девиз Лакана «назад к Фрейду». Используя минималистский формализм в соответствии с логикой расположения, Лакан фокусируется на основах стандартной психоаналитической модели, которая артикулирует образование первичной идентификации субъекта (аутоэротизм, введение в нарциссизм, стадия зеркала, идеальное я) — субъекта сексуированного, вписанного в линию поколений элементарных структур родства (Эдипов комплекс и кастрация, запрет на прикосновение/инцест, Я-Идеал), — и включает в себя проверку реальности, приобщающую к культуре, воспитывающую и обеспечивающую реальное бытия человеком. (Прим.перев.: Термин реалитэтспрюфунг (нем.Realitätsprüfung) введён Фрейдом в работе «Положение о двух принци­пах психической деятельности» 1911 г.)

Примечание Ж. Лакана к тексту «О вопросе, предваряющем любое возможное лечение психозов» 1958 г., датируемое от июля 1966 г.[2], неизбежно привлекает внимание клиницистов.

Это примечание предлагает должным образом преобразовать схему-R в вещественную проективную плоскость. Строго говоря, Лакан оставил открытым вопрос относительно нечётного числа полуоборотов упомянутой ленты Мёбиуса, от которого зависят вариации погружения проективной плоскости в Декартовом пространстве R3, между кросс-капом (bonnet croisé), Римской поверхностью Штейнера и поверхностью Боя.

[Прим.перев.: Бонé круазé (фр. bonnet croisé) — альтернативное название фигуры кросс-кэп, в переводе с французского «скрещенная шапочка» или «скрещенный колпак». В терминологии отечественной топологической школы этот объект называют пленкой Мебиуса.]

Тем не менее, именно кросс-кэп появляется у Лакана впервые во время семинара «Идентификация»[3], и используется в дальнейшем во всём его учении. И именно трансформацию схемы-R в кросс-кэп применяют, особое внимание уделяя её развитию, ученики Лакана, среди которых: Пьер Сури, Жан-Мишель Вапперо, Рене Лью, Жан Лафон, Франсуа Рэно, Серж Коте, Эрик Лоран, Этьен Жильсон, Пьер Сибони и др.

На рисунке 1 представлено что-то похожее на два эталонных способа получения замкнутого проективного пространства. Первый — путём сшивания двустороннего самопересекающегося диска с лентой Мёбиуса, независимо от числа полуоборотов. [Прим.перев.: Число полуоборотов должно быть нечётным.] Второй способ — сшивание двустороннего диска с самопересекающейся лентой Мёбиуса, вновь независимо от количества полуоборотов.

Поверхность Боя получается по такой же технологии, за исключением того, что в связи с её конструкцией необходимо три полуоборота ленты Мёбиуса, а не один, как в случае с кросс-кэпом.

Как писал великий математик и христианский моралист Блез Паскаль в своих письмах к провинциалу[4]: «я никогда не обсуждаю слова, пока не договорюсь об их значениях». Теперь нам известно, что даже в математике этот постулат здравого смысла не лишен двусмысленности. Но, по его примеру, следует различать топологически разные точки зрения, чтобы уменьшить путаницу в отношении понимания характеристик поверхностей, к которым трудно интуитивно получить доступ, тем более, что разные точки зрения обогащают и обновляют многие фундаментальные концепции психоанализа, такие, как перенос, контрперенос, интерпретация (хирургия поверхностей), объектные отношения и т.д.

Экстренсек: Поверхность рассматривается извне, из пространства представления, которое ее содержит. Именно в этом типе переноса аналитик оказывается внешним по отношению к субъективности пациента

Интренсек: Поверхность рассматривается исходя из нее самой, без учёта окружающего её пространства. Другими словами, как если бы бесконечно плоское существо, лишенное толщины[5], перемещалось бы не по-, но в- поверхности, как чернильное пятно впитывается в структуру промокательной бумаги (аналогия не совсем точна, поскольку поверхность не имеет толщины). [Прим.перев.: Чтобы представить положение вещей, предлагаем сравнить шар и сферу. Сфера не имеет плотности, она является поверхностью, а шар — это тело. Поверхность задана двумя координатами — х и у, а толщина уже не является поверхностью.] Здесь мы наблюдаем субъективность пациента в его отношении к самому себе, к подобным ему и к реальности, к которой он имеет доступ. Учитывая, что ему может быть очень трудно определить, на каком типе поверхности он передвигается, он остаётся неочевидным для самого себя. Тем более, когда это такие неориентируемые поверхности как лента Мёбиуса, кросс-кэп или поверхность Боя.

Локально, снаружи или изнутри: принимается во внимание только часть поверхности. Для неориентируемых поверхностей характерно то, что локальные свойства и характеристики поверхности не совпадают с глобальными свойствами и характеристиками поверхности. С внутренней точки зрения, субъект сталкивается с препятствиями для глобального восприятия поверхности на которой он передвигается. С точки зрения аналитика, экстренсек, степень, значение и функция видимого им локально симптома не совпадают с его функцией, исследуемой с глобальной точки зрения.

Глобально, снаружи или изнутри: Поверхность рассматривается в своей целостности; что касается неориентируемых поверхностей, свойства, которые локально их характеризуют, не идентичны их глобальным свойствам (например, локально, лента Мёбиуса является двусторонней, и глобально — односторонней: при определенном рассмотрении сумма её частей не равна целому).

Рассмотрим теперь замкнутую поверхность сферы. Её удобно представить снаружи, расположенную во включающем её окружающем пространстве — в котором есть как минимум три измерения — том самом, в котором привычно «передвигаться» или «эволюционировать» в масштабах человеческого мышления. [Прим.перев.: Эволю (фр. évoluer) одновременно означает как перемещаться, так и эволюционировать. Автор уже использовал этот глагол в примере с плоскими существами, здесь он продолжает аналогию.]

Благодаря некоторым уловкам перспективы, иначе говоря, проективной геометрии, возможно это представить на двухмерной поверхности бумаги. Наше видение, наше воображение, наше понимание не ограничены такими операциями, которые появляются как очевидные со времен Возрождения, а скорее всего, еще и с Античных времён. [Прим.перев.: В античности существовало представление о линейной перспективе, однако такого понятия, как единая точка схода, особенно, его необходимости не существовало. Подробнее см. Панофский Э., «Перспектива как символическая форма».]

В случае с кросс-кэпом или поверхностью Боя это не так, поскольку их закрытие в замкнутую поверхность в окружающем их пространстве, экстренсек всегда требует четырёх измерений.

Как бы мы не желали и не старались [это представить], за исключением некоторых одаренных воображением товарищей, среди которых, несомненно, Ж.П.Пёти, наше [человеческое] воображение и наше понимание, на этот раз, бессильны: мы потрясены и сталкиваемся с ограничениями. Только аналогия[6] и математический формализм, в строгом смысле, позволяют убрать ограничения нашего интуитивного восприятия.

Ленты Мёбиуса с одним или тремя полуоборотами, в силу нечётного их количества, объединяют лицевую и изнаночную стороны ленты. Глобально, поверхности лент имеют только одну сторону и один край: они называются односторонними[7] и неориентируемыми, что как минимум озадачивает. Хотя король математиков Гаусс мог заметить такие математические объекты и раньше, их понимание не восходит дальше, чем к середине 19в.[8]

Эти незнакомые и удивительные для Античной Греции объекты [Прим.перев.: в качестве иллюстрации предлагаем читателю взглянуть на Римскую мозаику III века нашей эры с изображением кольца, свернутого как лента Мёбиуса, из мюнхенской Глиптотеки.] познания по многим направлениям наших сегодняшних знаний остаются непереходимыми, исключая фрейдовские этику и бессознательное.

Важно, что существование ленты Мёбиуса не может быть поставлено под сомнение или оспорено. Помимо того, что она существует математически, что можно доказать и подтвердить, такую ленту можно сконструировать физически, материально и наглядно в нашем трехмерном пространстве. Короче говоря, перед нами все компоненты случившегося парадокса[9].

Используем аналогию. Реализуя некоторые корректно примененные непрерывные деформации, легко преобразовать двусторонний цилиндр в сферу, то есть в замкнутую поверхность в окружающем пространстве R3. Когда мы хотим произвести ту же трансформацию с лентой Мёбиуса, ее глобальная характеристика быть, экстренсек, односторонней, её отношение внутреннего и внешнего, наследуется кросс-кэпом или поверхностью Боя.

В случае с кросс-кэпом и поверхностью Боя, хотя они и замкнуты, внутреннее и внешнее пространства остаются неразделенными.

Как мы можем заметить, снаружи её замкнутость радикально отделяет внутреннее пространство от внешнего. В случае с кросс-кэпом и поверхностью Боя, хотя они и замкнуты, наоборот, внутреннее и внешнее пространства остаются неразделенными.

Эти топологические модели позволяют нам, таким образом, уловить единосущную связь между замкнутой поверхностью и принципом реальности Фрейда[10], частичной потерей контакта с реальностью[11] и попыткой его, этот контакт, возобновить через конструкцию нео-реальности[12]. Дело не только в принципе удовольствия, благодаря которому выстраиваются границы Себя и не-Себя, то есть первые основания идентичности, но и в переживаниях печали (травма рождения Ференци или Ранка[13]), неудовлетворенности, страдания и неудовольствия.

Независимая реальность, первоначальное внешнее, чужеродность и несходность, задержка удовлетворения потребности, галлюцинаторное удовлетворение в качестве эрзатц, дар любви, или ненависти, или невежества [Прим.перев.: Любовь, ненависть и невежество для Лакана — три основные страсти, он упоминает это, например, в 17ом семинаре и в тексте «функция и поле речи и языка в психоанализе».], подчиненный закону каприза или постоянству воспитывающих родителей, — всё это в сущности предстаёт как инородное тело, навязчивое, преследующее, даже угрожающее, которое учреждает субъект или препятствует его конституированию.

В других терминах это можно описать через бета элементы[14], которые подлежат отрицанию, удалению через проективную идентификацию и даже радикальному отбрасыванию до любого суждения атрибуции или возможного существования[15].

Изложенное выше в общих чертах позволяет установить более или менее четкое различие между тем, что является внутренним для субъекта и внешним по отношению к нему, а также определить, что исходит от субъекта, а что снаружи.

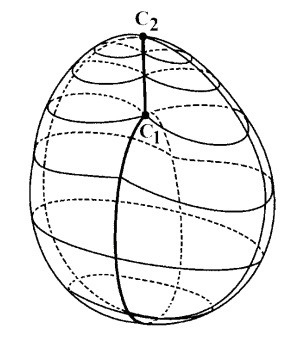
Тем не менее, в отличие от сферы или тора, которые претерпевают изменения естественным образом в трехмерном пространстве репрезентации, для представления кросс-кэпа и поверхности Боя как в трехмерном пространстве, так и в двумерном (на бумаге), требуются дополнительные уловки.

Что касается кросс-кэпа, этих уловок три: речь идет о особенностях свойственных погружению кросс-кэпа в трехмерное пространство R3 и в двумерное пространство R2 (рисунок 2).

В числе этих трех особенностей две крайние точки С1, С2 и линия самопересечения [Прим.перев.: оригинальный термин «ligne d’auto-intersection»], или, по-другому, пересекающая-себя-линия [Прим.перев.: оригинальный термин «la ligne d’auto-traversée»].

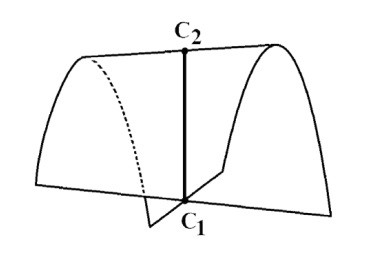
Точки С1 и С2, которые ограничивают линию самопересечения, являются так называемыми points cuspidaux, или точками пинча [Прим.перев.: Пуан куспидо (фр. Points cuspidaux) — точки Пинча на французском].

Мы также называем их сингулярности Уитни, в честь математика, который определил их как точки поверхности, не имеющие касательной плоскости, в противоположность другим точкам, составляющим поверхность (рисунок 3). Любая окрестность таких точек пинча самопересекается. Также говорят о точке возврата, каспе, складке.

Линия самопересечения обозначает явление самопересечения поверхности с самой собой, без нарушения непрерывности. Она демонстрирует те же самые свойства, что и точка пинча, но в этом случае они относятся к линии.

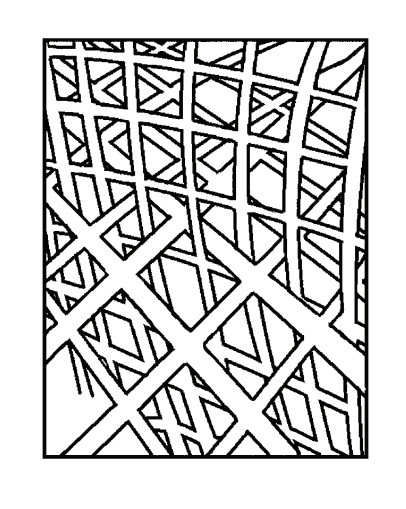
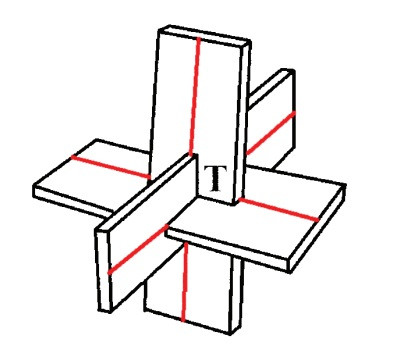
В своей работе Topologicon[16] Жан-Пьер Пёти ловко предлагает изобразить эту линию (самопересечения) как место, где пересекаются, например, две поверхности решетки (рисунок 4), но без возможности пройти от одной части поверхности к другой, то есть без разрывов.

Именно через эту линию самопересечения связываются внутренняя и внешняя части замкнутой поверхности кросс-кэпа.

По правде говоря, предыдущие формулировки этих трех особенностей, в действительности появляются лишь тогда, когда мы помещаем кросс-кэп в пространство репрезентации размерностью ниже, чем четырехмерное, с экстренсек точки зрения. Если это забыть, они окажутся слишком приблизительными и даже, в некотором смысле, ложными.

Более уместно утверждать, что свойство непрерывности перехода между внутренней и внешней частями замкнутой поверхности кросс-кэпа не локализуется в одной линии и двух уникальных точках, а содержится глобально в каждой точке поверхности, если рассматривать кросс-кэп интренсек, вложенным в естественное для него четырехмерное пространство репрезентации. [Прим.перев.: При погружении не допускается точек самопересечения, а при вложении — допускаются.]

Напротив, будучи погруженными, эти особенности составляют что-то вроде квалисигнумов[17], которые следует отображать и добавлять на рисунок, чтобы интерпретировать его в трех или двух измерениях. [Прим.перев.: Квалисигнум (фр. qualisigne) — одна из категорий знаков у Ч.Пирса. Качество, используемое как знак. Например, красный цвет, цифра 13. Подробнее см. Боброва А. С., «Логика и возможности иконического анализа рассуждений» // ΠΡΑΞΗΜΑ. 2021. № 1 (27). С. 7–24]

Но не следует заблуждаться: эти три особенности, тем не менее, представлены на таком уровне существования, из которого вытекает, что они не могут считаться фиктивными, искусственными или нереальными. Они тоже реальны, поскольку они изображают на чертеже кросс-кэпа в двух или трех измерениях его реальное свойство — быть замкнутой топологической поверхностью, непрерывно соединяя его внутри и снаружи.

Чтобы не пребывать в недоумении относительно точки пинча, которую не использует Лакан, топологизируя схему-R, Пёти открывает для него существование другой поверхности. Речь идет о погружении поверхности Боя.

Чтобы не пребывать в недоумении относительно точки пинча, которую не использует Лакан, топологизируя схему-R, Пёти открывает для него существование другой поверхности, замкнутой, демонстрирующей непрерывный переход между внутренним и внешним, но представляющей только две особенности.

Речь идет о погружении поверхности Боя (рисунки 5 и 6).

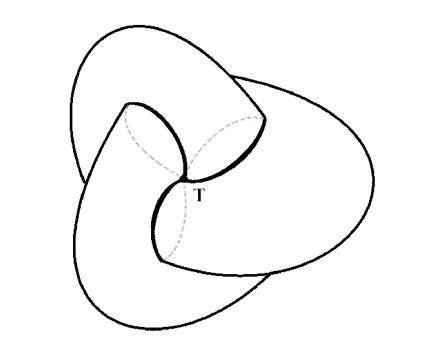
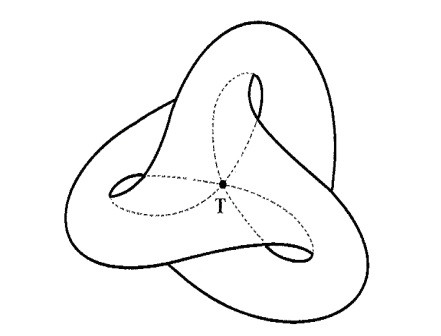
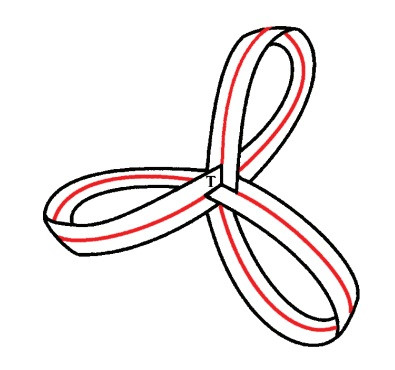
Две особенности этой поверхности представлены линией самопересечения, принимающей форму трех петель, напоминающих клевер (на рисунке 5 это сплошная линия, на рисунке 6 это пунктир) и тройной точкой T (рисунки 7 и 8).

Исходя из этого указания, на рисунке 9 ниже нами представлен первый результативный, насколько нам известно, вариант топологизации схемы-R в поверхность Боя[18].

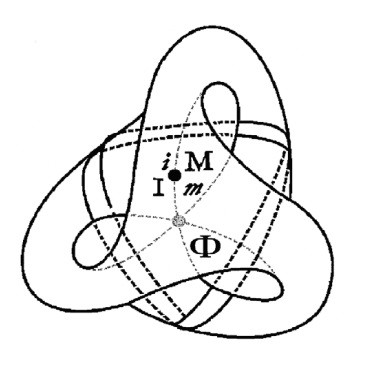
Чтобы понять эти тонкости, преодолеть сложности, возникающие при ее осмыслении, и лучше судить о потенциальных преимуществах, которые должна была бы привнести поверхность Боя, требуется рассмотрение деталей двух возможных способов трансформации схемы-R в поверхность Боя.

Трансформация схемы R на поверхности Боя при рассмотрении схемы R в качестве двустороннего диска и расположении символического фаллоса в тройной точке Т

Ниже на рисунке 10 показаны различные этапы данной трансформации, сосредоточенные в тройной Т-точке, созданной погружением, если смотреть снаружи — сначала сверху, а затем снизу. [Прим.перев.: Для полноты понимания процесса выворачивания мы приводим иллюстрацию из работы Бернарда Вандермерша «Кросскап Лакана или “Асфера”», опубликованной в 2008 году.]

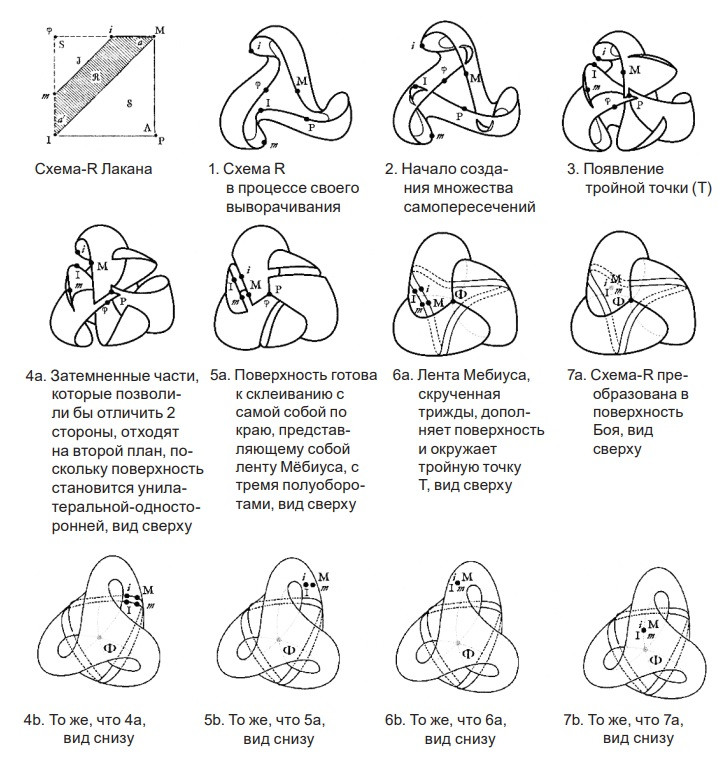
Таким же образом, как Лакан расположил символический фаллос (Ф), в соответствии с конъюнкцией или сгущением (отцовская метафора) Имени-Отца (P) с воображаемым фаллосом (ϕ) в точке С1 на кросс-кэпе, (Ф) может отождествляться с тройной точкой T на поверхности Боя, где перекрещиваются три линии самопересечения трех конститутивных петель поверхности.

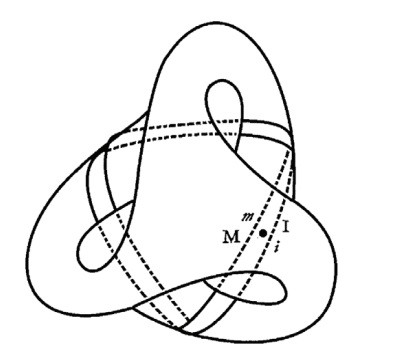
Также можно обнаружить конъюнкцию других четырех элементов схемы R: я (m), зеркальный образ (i), мать (M) и Я-идеал (I), которые, будучи снабжены векторами, исходя из схемы R, сливаются не после одного полуоборота ленты реальности miMI, как в случае с кросс-кэпом, а после трёх полуоборотов, свойственных поверхности Боя. Этот аспект проиллюстрирован на рисунке 10 за счёт того, что лента Мебиуса с тремя полуоборотами может без разрывов быть наложена на поверхность Боя, окружая тройную точку (Ф).

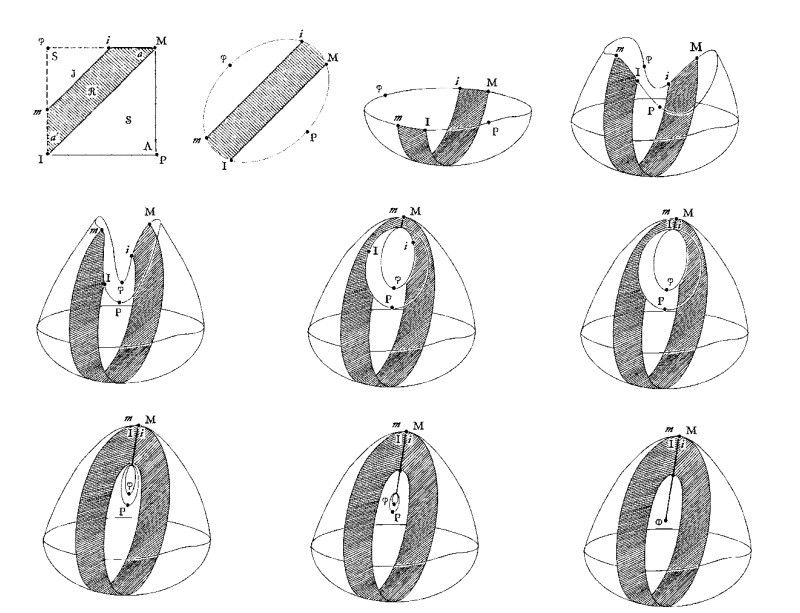
Трансформация схемы R на поверхности Боя из ленты реальности, (рассматриваемой в качестве ленты Мебиуса с тремя полуоборотами) располагающей символический фаллос в тройной точке T

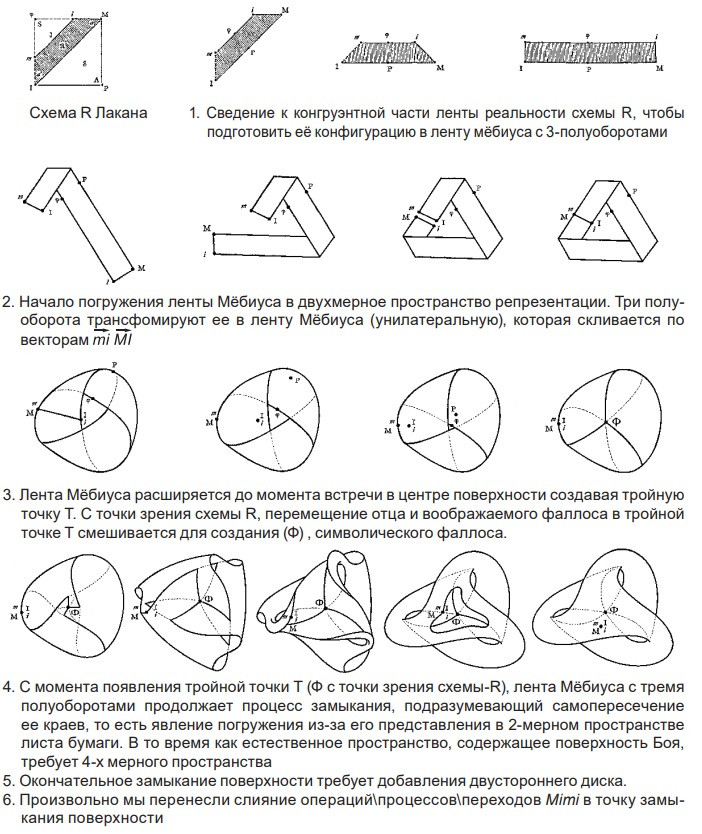
Точно так же, как можно построить кросс-кэп из ленты Мебиуса c одним полуоборотом, как показано на рисунке 2, мы покажем на рисунке 11 как можно создать поверхность Боя с ее тройной точкой T из ленты реальности mi, MI, рассматриваемой как лента Мёбиуса с тремя полуоборотами.

При рассмотрении снизу (рисунок 12) из–за прозрачности [фигуры] становится доступной взгляду тройная точка Т, то есть символический фаллос, которая концентрирует отцовскую метафору. Другими словами, она топологически возникает из–за сгущения между Именем-Отца и воображаемым фаллосом, чтобы придать облик значения загадочному желанию матери по отношению к зарождающемуся субъекту.

При рассмотрении снизу (рисунок 13) мы находим комплекс MimI, сведенный к точке, через которую проходит лента Мёбиуса с тремя полуоборотами, то есть лента реальности схемы-R.

Лента обрамлена и, следовательно, ограничена регистрами воображаемого и символического, которые содержат и смягчают требование Реального к немедленному удовлетворению.

На самом деле, основная функция комплекса MimI, стадии зеркала, а затем комплексов Эдипа и кастрации, посредством конституирования рамки фундаментального фантазма, состоит в том, чтобы умерить принуждение со стороны Реального к повторению (возвращению к тому же самому).

Фантазм и реальность, реальность в качестве гримасы Реального[19], открывают доступ к повседневной реальности человека и его более или менее «переносимым» взлётам и падениям [Прим. перев.: В этом отрывке автор ссылается на труд З.Фрейда «Недовольство культурой» — Малаз дан ла сивилизасион (фр.Malaise dans la civilisation), что дословно переводится как «боль в цивилизации»].

Можно считать, что цель данной статьи достигнута. Мы подробно показали некоторые возможные пути преобразования лакановской схемы-R в поверхность Боя.

Другими словами, благодоря предложению Пёти и пути, открытому Лаканом, мы располагаем наброском математизации стандартной психоаналитической модели, демонстрирующей фундаментальные операторы, задающие предположение о субъекте, способном взять на себя свои обязанности, любить, при необходимости, создать семью, работать, играть и творить[20].

Логическое продолжение этой презентации отныне должно привести нас к развитию преимуществ, которые математическая модель привносит в актуальное, динамическое и экономическое понимание основы субъекта фрейдовского бессознательного.

Но также важно задать вопрос, как мы можем применить полученные представления о кросс-кэпе или поверхности Боя для понимания психотических структур, представленных в работе Лакана «О вопросе, предваряющем…» и причастных, в его подходе, к отбрасыванию Имени Отца? В частности, в отношении потери контакта с реальностью (заблуждения, галлюцинации, более или менее непоколебимая уверенность, passage à l’acte). [Прим.перев.: Термин пассаж эль акт, фр., «переход к действию», обычно не переводят.]

Однако, мы вынуждены оставить такое рассмотрение на потом, ведь к краям психоаналитического реального, которое нам иногда удается уловить, как и к фрагментам реального, в которое пытаются проникнуть, охватывая его, буквы и математические числа, нельзя подойти так легко, как можно было бы подумать, мысля «по-человечески».

Немаловажно, что вследствие этого возникает одна загвоздка. Если более тщательно подойти к описанию трех встреч Лакана-Пети обнаруживается серьезная трудность, которую нельзя, честно говоря, обойти молчанием: в разработке Жан-Пьера Пети скрытно проскальзывает двусмысленность, которая вполне может поставить под сомнение идею, которую, с его слов, он предоставил Лакану.

На предыдущих схемах, на которых показаны два наиболее прямых пути превращения схемы-R в поверхность Боя, внимательный читатель заметит, что мы расположили символический фаллос на уровне сингулярности T, то есть тройной точки, с которой сопоставлена линия самопересечения в форме клевера.

Однако в тексте повествования о трех встречах Жан-Пьер Пети вводит дополнительный математический оператор для поверхностей в целом и для поверхности Боя в частности: понятие полюса.

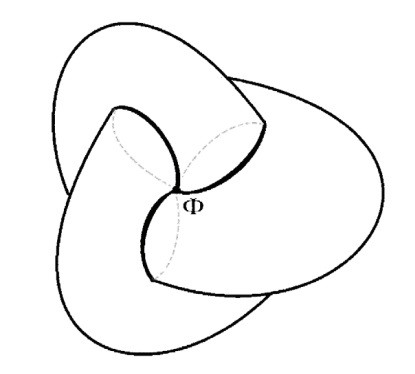
И именно на уровне этого полюса (рисунок 14), который можно достать, как кролика из шляпы, из поверхности Боя, а не на уровне сингулярности тройной точки T, он предлагает расположить символический фаллос.

Артефакты, связанные с погружением (точки Пинча и линия самопересечения кросс-кэпа, тройная точка и линия самопересечения в форме клевера на поверхности Боя), во многом характеризуют внутренние и фундаментальные свойства этих поверхностей, появляющиеся локально только при погружении, но присутствующие глобально при вложении в свойственных им (4-х мерных) пространствах, как мы уже обсуждали выше.

Хотя математическое понятие полюса не является, строго говоря, топологическим, а в большей степени относится к геометрическому подходу, эти две дисциплины, в то же время, тесно связаны. Так или иначе, понятие полюса нельзя рассматривать математически как характеристику, присущую поверхности интренсек. Для ее или их появления требуется сетка (нанесение на поверхность меридианов), которая будет наноситься на поверхность снаружи как при плетении изделий.

Топологически только характеристика Эйлера-Пуанкаре[21] позволяет различать и классифицировать поверхности независимо от того, являются ли они ориентированными или нет.

Мы не вдаёмся в подробности вычисления этой характеристики Х, которая раскладывает их на количество вершин или точек S, минус количество рёбер А, плюс количество граней F.

X= S–A + F

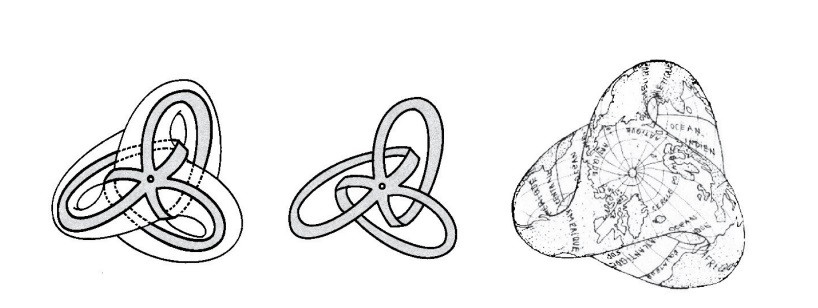
На приведенном ниже рисунке 15, которым мы обязаны Пёти, мы можем более тонко интуитивно понять нюансы поверхности Боя, а также проиллюстрировать, как создать единый полюс этой поверхности, применив к нему мёбиусовы Меридианы. С помощью шутки или поэзии, а также своего доказанного вкуса к научной фантастике он показывает нам, какой была бы наша планета Земля, если бы она была структурирована как поверхность Боя. Это распространяется и на его нынешние работы, в которых он предлагает структуры, альтернативные актуальному пониманию Вселенной, в соответствии с неортодоксальными путями в отношении доминирующих парадигм современной астрофизики.

Однако, возвращаясь к нашей теме, невозможно не задаться строгим вопросом относительно этой замены между точками Пинча кросс-кэпа и введением уникального полюса на поверхности Боя, которую Пети предложил Лакану, чтобы выбрать поверхность с единственной присущей ему особенностью погружения. Не очевидно, почему он не ограничивается тройной точкой T на поверхности Боя, чтобы разместить символический фаллос, как мы показали на рисунках 8, 9, 10, 11 и 12.

Также Пети забывает упомянуть или сообщить Лакану, что у самого кросс- кэпа, как и у поверхности Боя, есть один и только один уникальный полюс (рисунок 16).

Тот факт, что обе эти поверхности имеют один единственный полюс, лишает как одну, так и другую поверхность привилегий в том, чтобы оказаться более законной или оправданной для топологизации схемы-R

Из этого следует, что, если мы признаем, что особенности, вытекающие из погружения кросс-кэпа и поверхности Боя, являются вторичными, переходными или вспомогательными, какими их считал Пёти, тот факт, что обе эти поверхности имеют один единственный полюс, лишает как одну, так и другую поверхность привилегий в том, чтобы оказаться более законной или оправданной для топологизации схемы-R.

Пёти мог бы с таким же успехом предложить Лакану расположить символический фаллос на единственном полюсе кросс-кэпа, в то же время указав ему, что особенностями, возникающими после погружения в эту поверхность, можно пренебречь, или даже что они не имеют достаточной ценности, чтобы вместить основные операторы схемы-R.

Т.о. мы обнаруживаем произвольный или даже условный характер выбора любой из этих поверхностей для топологизации схемы-R, что в то же время подтверждает, что кросс-кэп так же уместен для поддержки основных операторов схемы-R, как и поверхность Боя. Тем более, что опытный читатель без особых трудностей согласится с тем, что кросс-кэп, несомненно, легче понять интуитивно, чем поверхность Боя.

Тем не менее, чтобы оставаться строгими и исчерпывающими, мы все равно представим на следующих двух рисунках, 17 и 18, этапы трансформации схемы-R в поверхность Боя, где символический фаллос находится не в тройной точке T, а в месте полюса, как Пети рекомендовал Лакану во время их встреч.

Мы используем два способа получения поверхности Боя, упомянутые ранее: либо наложение шва на двусторонний самопересекающийся диск на ленту Мебиуса с тремя полуоборотами для первого способа (рисунок 17), либо наложение шва на самопересекающуюся ленту Мебиуса с тремя полуоборотами, из двустороннего диска для второго способа (рисунок 18).

Преобразование схемы-R в поверхность Боя, рассматриваемой как двусторонний диск, где символический фаллос находится на уникальном полюсе поверхности

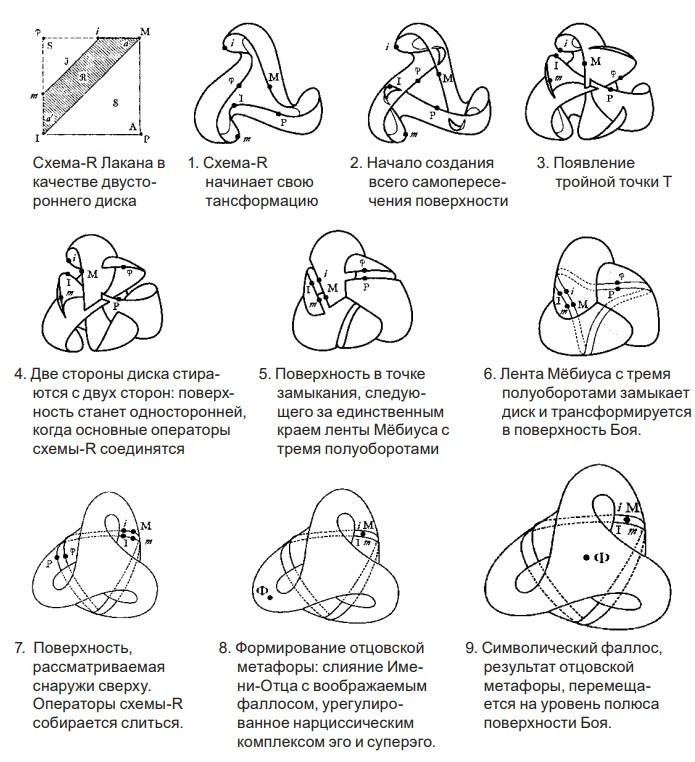
В этом первом случае, опять же, схема-R эквивалентна двустороннему диску. Путем последовательных искажений, включающих пересекающий-себя диск, и с учетом того, что основные операторы схемы-R оказываются сопоставленными непосредственно перед замыканием поверхности, соответствующей ленте Мебиуса, мы успешно достигаем погружения поверхности Боя, причем конденсация операторов имени отца и воображаемого фаллоса актуализируется не на уровне сингулярности тройной точки T, а на уровне единственного полюса поверхности.

Преобразование схемы R в поверхность Боя из ленты реальности, спроектированной как лента Мебиуса с тремя полуоборотами, где символический фаллос находится на уникальном полюсе поверхности

Второй пример также требует редукции схемы-R до наиболее похожей формы ленты без потери основных операторов схемы-R, что позволяет применить к ней три полу-скручивания и наделяет её свойством быть односторонней.

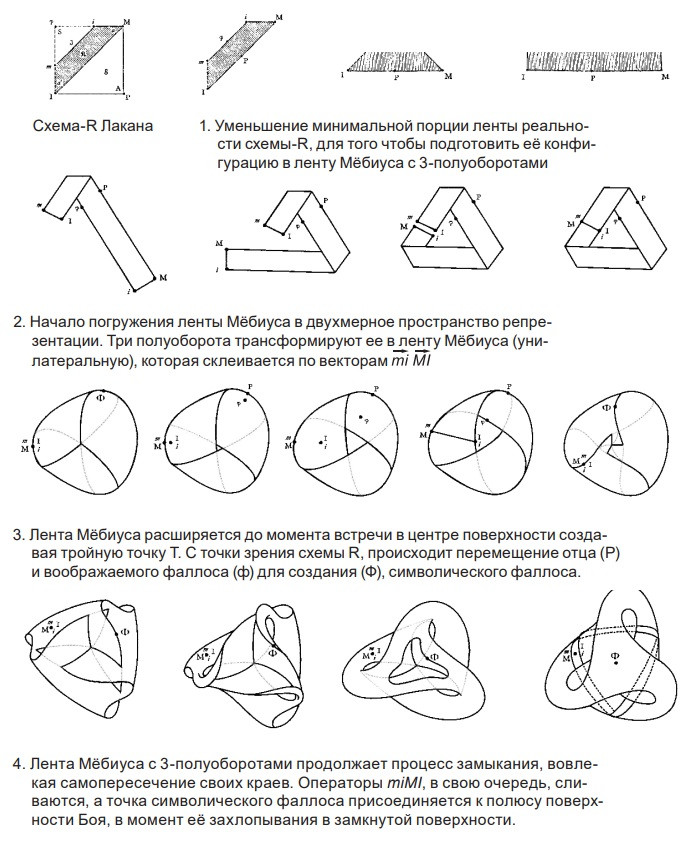
Лента расширяется до самопересечения, создавая тройную точку T, начало погружения поверхности, которое будет закрываться присоединением двустороннего диска. На этот раз конденсация имени отца и воображаемого фаллоса происходит путем миграции двух операторов не в тройную точку T, а в уникальный полюс поверхности Боя.

В качестве вступительного слова мы напомнили, что схема R представляет собой сборку или набросок лакановского девиза «назад к Фрейду!», который извлекает неприводимые элементарные частицы для осуществления эффективной субъективности, более менее тонко, критично и ненадежно сплетённой влечениями жизни и смерти [22].

Фрейдистская во всех отношениях схема сформулировала психоаналитическую ортодоксальность, основанную на концепциях бессознательного, комплексов Эдипа и кастрации (метафора отца, имена-Отца), аутоэротизма, первичного и вторичного нарциссизма, объектных отношений (стадия зеркала, лента реальности miMI), наконец, переноса и контрпереноса, введенных с первого поколения психоаналитиков, во главе с Ференци[23].

Что дают топологические модели, будь то кросс-кэп или поверхность Боя, для интерпретаций, открытых посредствам схемы-R?

Во-первых, то, что травмы, отклонения и скорби субъективности, нормированные в невротическом режиме от нормального до патологического, подразумевают психическую замкнутость, возникающую из неориентирумой поверхности и обеспечивающей внутреннюю и внешнюю непрерывность. С другой стороны, отбрасывание имени отца приводит к невозможности замыкания таких поверхностей, что приводит к несоответствию в учреждении идентичности, способной присвоить себе любое явление ксенопатического. [Прим.перев.: Ксенопатия от греч. xаenos — чужой + суффикс -pathie, от греч. ἀ π ά θεια, apatheia, означающий состояние или болезнь в медицинском дискурсе; феномен, при котором больной воспринимает то, что он ощущает, как исходящее не от него самого, а как приходящее извне, навязанное ему другими.]

Эта замкнутость неориентируемых поверхностей во многом соответствует эффективности принципа реальности, в терминах Фрейда. Это не что иное, как обеспечение непрерывности внутреннего и внешнего на замкнутой, односторонней, с глобальной точки зрения, и двусторонней, с локальной точки зрения поверхности. Либо то, что посредством травм, фаз, стадий, ключевых структурных элементов будет происходить через последовательное переживание различных модальностей отсутствия (лишение — фрустрация — кастрация), связанных с мгновенным наслаждением, установлением границы (фильтрация, торможение и возбуждение, разграничение, стимульный барьер) между внутренним и внешним миром. [Прим.перев.: Термин «стимульный барьер», пар экзитатион (фр.pare-exаcitation), в оригинале нем. райцшутц (нем. Reizschutz) впервые введён З.Фрейдом в работе «По ту сторону принципа удовольствия».]

Кроме того, это закрытие односторонней поверхности совпадает с реализацией комплекса miMI и сгущением точки Имени-Отца с точкой воображаемого фаллоса, что позволяет дать топологический взгляд на проблемы стадии зеркала, комплексов Эдипа и кастрации и фундаментальный фантазм. Иначе говоря, замыкание односторонней поверхности иллюстрирует значимость отцовской метафоры, т.е. вписывания символической фаллической позиции в качестве модальности нехватки, отделяющей фиксацию ребёнка на воображаемом фаллическом объекте. Этот объект, предположительно, насытил бы загадочное желание матери для её детей: cкончаться, cном забыться, уснуть… и видеть сны?… [24] — Иметь иль быть? Лакана гений наравне с Шекспиром. [Прим. пер. — Фабрис Гийо цитирует и обыгрывает здесь Гамлета, в оригинале: mourir, dormir, rêver peut-être].

Поверхность Боя обладает тем преимуществом, что материализует модель, подчеркивающую важность Эдипова периода путем установления символического фаллического ориентира, идентифицированного с уникальной особенностью поверхности (полюсом или тройной точкой T). Тем не менее, эта поверхность может отодвинуть на второй план роль второго оператора в реализации замыкания поверхности, которая проявляется в диалектике векторов MImi, стадии зеркала, в качестве неизбежного момента в основе предрасположенной субъективности, создающей синтез между аутоэротизмом и нарциссизмом, частичным объектом и принятием целого, первым решающим этапом, но еще не завершенным шагом в различии между внутренним и внешним.

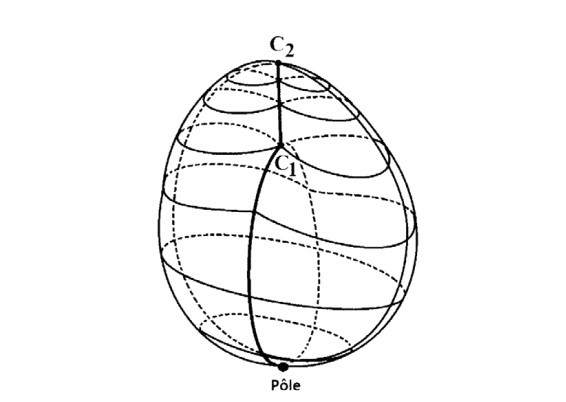
Соответственно, та самая точка Пинча в верхней части кросс-кэпа, C2, могла бы быть вполне подходящей для получения этой узловой точки зеркальной стадии, т.е. слияния векторов MimI, чтобы подчеркнуло бы ее столь же фундаментальную важность, как и самой отцовской метафоры (рисунок 19).

Необходимость рассматривать эти два, структурирующих схему-R, комплекса в равной степени важна, когда речь идет именно о рассмотрении логических последствий, влияющих на один или оба из этих двух основных комплексов в клинике.

Для примера разработка примечания, предложенного Лаканом, которое до этого времени могло считаться второстепенным, виртуозно иллюстрирует нам замечание выдающегося клинициста Жан-Клода Мальваля, который указывает, что мы принадлежим к золотому веку медицинской психиатрии и нам удается точно определить различные психопатологические комбинации психотических структур в соответствии с эволюционной шкалой бреда[25].

Топологически, начиная с модели кросс-кэпа, отбрасывание имени отца[26], P0, приводит к не-сгущению точки P (Имени-Отца) и точки воображаемого фаллоса, начиная с уменьшающейся градации типов бреда, P3, P2, P1, P0, вплоть до более или менее продвинутой дезагрегации самого комплекса MimI (рисунок 20).

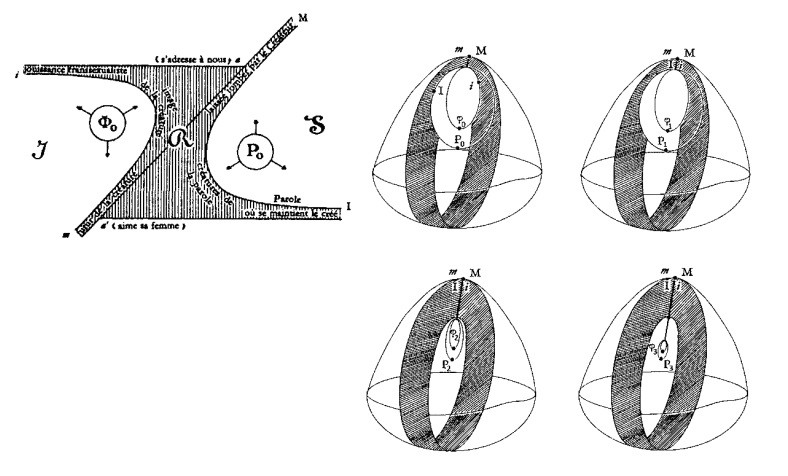
Но мы не будем углубляться в эту топологизацию схемы I психотических структур, поскольку она заслуживает отдельного и конкретного развития.

На этом этапе мы, наконец, достигли своих целей: показали два основных пути преобразования схемы R в поверхность Боя, в качестве альтернативы кросс-кэпу, как это было принято ранее в связи с прочтением Лакана, к которому мы привыкли. Рассказ о трех встречах Лакана и Пёти позволил подвергнуть сомнению этот установленный факт.

Тогда как Пёти ввёл экстренсек понятие полюса на поверхности Боя вместо того, чтобы прибегать к тройной точке Т как к свойству внутреннего погружения на поверхности, тень обоснованного недоверия упала на основательность его предложений относительно топологизации схемы R.

То, что мы не можем принять решение в пользу той или иной модели не столь важно. Главное, что нам предлагается возродить интерес к букве Лакана, который предложил нам прибегнуть к топологическим моделям, чтобы помочь понять задействованные психические процессы, происходящие в нашей повседневной клинической практике.

Наши выводы позволяют углубить различные подходы к обучению аналитиков и понимание путей передачи психоанализа, что могло бы ослабить сектантские и религиозные феномены, в тисках которых психоанализ всё ещё слишком часто находится, и, учитывая его значительный вклад в новую и беспрецедентную этику, вызвать больший социальный и политический интерес к созданию новых исторически уникальных взаимоотношений, которые могли бы обозначать своего рода «топологию Святого» [Etre un saint]. [27]

[Прим.перев.: Фабрис делает отсылку к главе 4 «Телевидения», где Лакан говорит следующее «Что касается меня, то я мыслю до умоисступления, ради того, чтобы подобные им (святым) появились вновь.]

Сноски автора:

1. Ж.-П. Пёти, Ф.Гийо «История трёх встреч Жана-Пьера Пёти и Жака Лакана развернувшихся вокруг поверхности Кросс-Капа и поверхности Боя», Фигуры психоанализа, № 14, 2006/2, стр. 181–204

2. Ж. Лакан, “Вопрос, предваряющий любое возможное лечение психозов” 1958 г., Париж, 1966 г, 553–334

3. Ж. Лакан, Семинар 9, Идентификация (1961–1962), 16 мая 62 г., не опубликован

4. Б. Паскаль, “О геометрическом уме и искусстве убеждать”, 1871 г., в завершенных произведениях, том 3, Париж, стр. 163-182

5. А. Пуанкаре, Наука и гипотеза, Париж, 1917 г., стр. 33

6. П. Сури, Цепи и узлы, часть 1, Париж, Изд. Мишель Томэ и Кристиан Леже, 1986–1988, стр. 36

7. А. Пуанкаре, “Analysis Situs”, Журнал политехнической школы, 1, 1895, стр. 1–121

8. Ж.К. Понт, Алгебраическая топология Пуанкаре, Париж, Пуф, 1974

9. Ф. Гийо, Психоаналитическая структура парадоксов — топология субъекта adhoc (лат. для этого случая/специально для этого) докторская диссертация по психоанализу на базе института Париж- 8, защита в 2002 г., под руководством Франсуа Рено и Сержа Коте

10. З. Фрейд, “Невроз и Психоз, 1924, о Неврозах, психозах и перверсии”, Париж, Пуф, 1992

11. З. Фрейд, “Психоаналитические заметки об одном автобиографически описанном случае паранойи — Шребер”, 5 Основных клинических случаев фрейда, Париж, Пуф, 1954

12. З. Фрейд, “Потеря реальности при неврозах и психозах”, 1924, о Неврозах, психозах и перверсии”, стр. 299–303

13. Ш. Ференци, Размышления о травматизме, собрание научных трудов, 4, Париж, Пайот, 1982, стр. 139–14

14. У.Р. Бион, Научение через опыт переживания (1962 г.), Париж, 1991

15. З. Фрейд, Отрицание, к результатам, идеи, проблемы, том 2, Париж, 1985

16. Ж.-П. Пёти, Топологикон, Париж, 1985, стр. 44

17. Ч.С. Пирс, Сочинения о знаке, собрание с переводом и комментариями Жерара Деледаля, Париж, Сёй, серия “L’ordre philosophique”, 1978

18. https://www.ecolefreudienne.fr/Fabrice-Guyod-Retour-sur-le-recit-des-trois-rencontres-de-Lacan-avec-Petit

19. Ж.Лакан, Телевидение, Париж,1974, стр. 67

20. З. Фрейд, “Психоаналитический метод”, техника психоанализа, Париж, Puf, 1970

21. Ж.-К. Пон, Алгебраическая топология от истоков до Пуанкаре, Париж, Пуф, 1974

22. З. Фрейд, По ту сторону принципа удовольствия, 1920, психоаналитические очерки, Париж, Payot, 1981 г., стр. 91

23. Ш. Ференци, Клинический Журнал, Париж, Payot et Rivages, 1932 г.

24. В. Шекспир, Гамлет, Полное собрание сочинений В. Гюго, Париж, Éditions Pagnerre, 1865, стр. 379 //

25. Ж.-К. Мальваль, Логика бреда, Париж, Masson, 1997

26. Ж.-К. Мальваль, Форклюзия Имени Отца, Концепция и её клиника, 2000

27. Ж. Лакан., Телевидение, стр. 28–28

_

Над переводом работали: Елена Янушковская, Александр Сильверстов.

Приносим благодарность Алексею Зайчикову за консультации и Марку Савичеву за предоставленный материал.